Tal como planteamos al final de la Parte 1 de este tema, tener controlados la mayor cantidad posible de aspectos relacionados a la definición de un alineamiento, requiere profundizar en los conocimientos de la programación en Lisp y tener claros los conceptos geométricos necesarios.
Las características geométricas del alineamiento estan influenciadas por los parámetros del diseño vial. Hay que tener presente el radio minimo para la velocidad de diseño, la longitud de la curva de transición, el sobreancho, el peralte para la curva, entre otros.
En principio, es adecuado fijarnos metas e ir de a pocos o por fases. Por ejemplo un primer objetivo sería:
- establecer algun modo de control que facilite la edición de curvas, si elijo una curva, ¿cómo puedo efectuar el cambio del radio sin tener que usar FILLET?
- que la modificación de la posición del PI actualice automáticamente el dibujo de los alineamientos concurrentes con la debida continuidad de las curvas adyacentes.
- que se pueda insertar un nuevo PI y el alineamiento se redibuje automaticamente
- que al eliminar un PI el alineamiento se redibuje.
Opciones para programar el control del alineamiento
Aún no se me han ocurrido otras opciones así que, se aceptan sugerencias factibles de implementar con lisp. Estas son las opciones que me he planteado:
- Mantener un listado de coordenadas de los puntos PI con sus parámetros, ya sea en un diccionario o un archivo externo
- incorporar los parámetros del alineamiento en la entidad de alineamiento (la polilinea) como XDATA
- administrar inserciones de bloques con atributos cuyos puntos de inserción coinciden con las coordenadas de cada PI.
Considero como más adecuada la última opción.
Administración de inserciones de bloque para controlar el dibujo de un alineamiento
Con una referencia de bloque con atributos se pueden guardar los datos que nos interesan:
- coordenadas del PI (con las coordenadas del punto de inserción)
- Radio de la curva (con un atributo)
- Sobreancho de la curva (con un atributo)
- Peralte de la curva (con un atributo)
- Longitud de la curva de transición (con un atributo)
- Nº del PI en la secuencia del alineamiento (con un atributo)
- Velocidad de diseño de la curva (con un atributo)
Las funciones a programar son muchas por las opciones a manejar durante un trabajo de edicion de alineamiento. En mi caso he llamado E-ALIN al comando que invoca al editor de alineamiento y presenta las siguientes opciones:
E-ALIN
Command: Cuadro/Suprimir/Mover/Insertar/Editar/estaKar/Refrescar/Guardar:
La opción "Cuadro" carga un cuadro de dialogo que muestra los datos de todos los PI del alineamiento. de acuerdo a la funcionalidad requerida ha llegado a tener el siguiente aspecto:
Tal cual me facilita varias operaciones, los efectos de los cambios que se efectúen solo serán "palpables" si se sale del cuadro con el botón Aceptar y luego se aplica la opcion Refrescar. Desde este cuadro no se modifican las posiciones de los PI.
El cuadro es muy interactivo y me permite controlar numéricamente los efectos de los cambios en el valor del Radio de la curva, de la longitud de la transición, de la Velocidad. Generalmente los valores del peralte y del sobreancho se calculan a partir del radio y la velocidad. En el caso de la longitud de la curva de transición también se hace un cálculo con el radio y la velocidad, se presenta en el cuadro para ser modificado si se requiere al igual que los demás parámetros. Al salir del cuadro se retorna a la lista de opciones:
Cuadro/Suprimir/Mover/Insertar/Editar/estaKar/Refrescar/Guardar:
Los cambios en la posición de los PI se hacen con Mover. Desde Autocad también se pueden mover las ubicaciones de los PI (comando MOVE) o editar los parámetros con el editor de atributos, los efectos se reflejan entrando a E-ALIN y escogiendo Refrescar.
Las demás opciones se explican por sí mismas, la opción Guardar es parte de un plan de contingencia, con esta opción se graba en un archivo de texto las coordenadas de los PI que definen el alineamiento, sus radios y longitudes de transición.
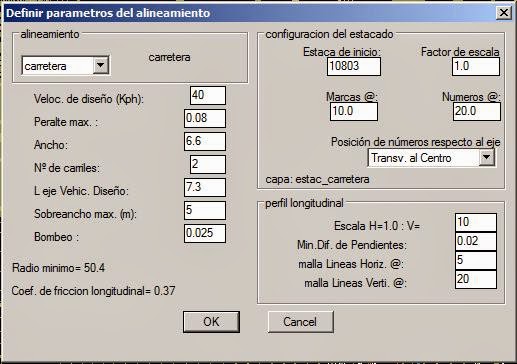
Para lograr este control de la información del alineamiento hay que tener almacenadas las características principales del diseño partiendo de una definición del alineamiento. Se puede programar una utilidad para este caso, y con la ayuda de un cuadro de dialogo como el siguiente, se facilitan las tareas:
Con las opciones que se presentan en el cuadro no se requiere de mayores explicaciones sobre lo que se puede hacer con él, el botón [Definir Parámetros] lleva a otro cuadro donde se definen los parametros del alineamiento:
Tambien se puede programar el dibujo de los bordes del alineamiento, en estos bordes debe reflejarse el desarrollo de los sobreanchos en las curvas.
El desarrollo de los sobreanchos
Cuando una curva requiere de un sobreancho Sa, se debe considerar la forma en que este se desarrollará desde un valor "cero" hasta el valor Sa. Es usual que el sobreancho debe desarrollarse en el lado interior de la curva, si el radio del eje Rc el radio del borde interior será Rbi = Rc - Ancho/2, la curva que desarrolla el sobreancho tendrá entonces como radio: Rbi - Sa. Las mejores opciones de desarrollo son:
- Mediante arcos, es decir se acomoda un arco de radio grande tangente al lado recto y tangente al arco central que describe el sobreancho.
- Mediante una clotoide que se desarrolla desde el tramo recto donde el radio es infinito hasta cuando el radio es Rbi - Sa.

He optado por usar la clotoide como transición para el desarrollo del sobreancho.
El proceso de cálculo consiste en hallar la longitud de la espiral necesaria para alcanzar la curvatura que produce el radio R= Rbi - Sa. Las relaciones que se deducen de la geometría correspondiente son las siguientes:
y(Q) = 2*R*Q*(Q/3 - Q^3/42 + Q^5/1320 - .....) (1)
R*cos(Q) + y(Q) = R + Sa (2)
y(Q) : representa el desplazamiento transversal de la clotoide para un angulo Q.
la combinación de las ecuaciones (1) y (2) nos llevan a obtener primero el valor de Q (el ángulo con la debida precisión) y luego la longitud de la espiral. Si el coseno se desarrolla como una serie, de la combinación de las ecuaciones de arriba es posible llegar a la siguiente relación:
Sa / R = Q^2 / (3*2!) - Q^4 /(7*4!) + Q^6 /(11*6!) - Q^8 /(15*8!) + . . .
El cálculo automatizado nos permitirá descubrir que si la curva tiene una longitud de arco muy pequeña, no se obtendrán desarrollos adecuados de la transición.
El desarrollo de la curva de transición para el eje del alineamiento mediante la clotoide será tratado en la siguiente entrada
Hasta Luego.